【航空機の運動解析ＫＭＡＰでは何ができるのか】

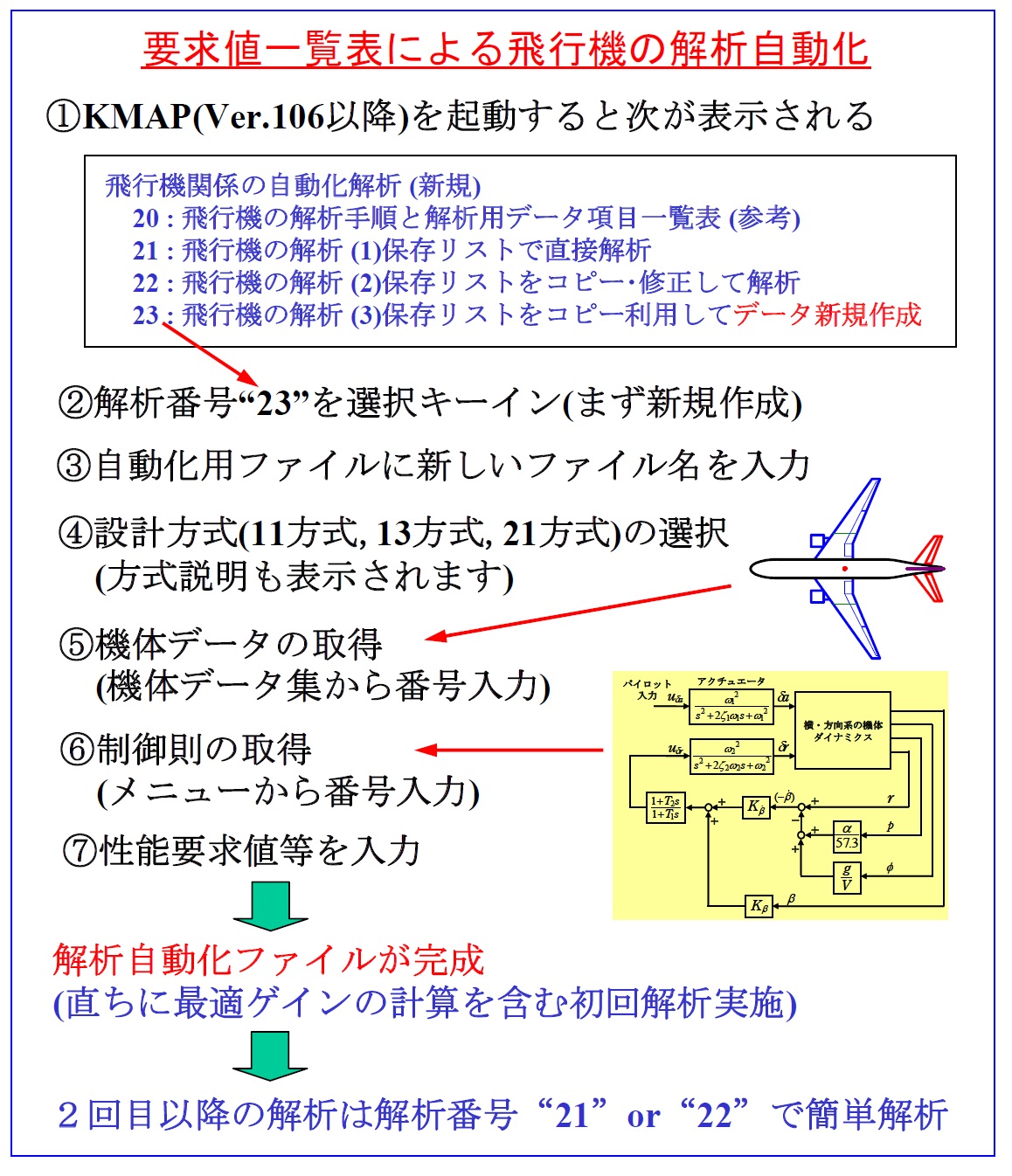
　設計解析プログラムＫＭＡＰは簡単に使うことができます．航空機の飛行制御問題だけでは
なく，自動車，船，水中ビークル，ロボット，工作機械などの制御問題，また振動工学の解析も
可能です．その他，構造物の弾性解析，流体力学の問題，熱の流れの解析，最適化の解析の
各種工学解析手法の基礎も例題を通して学ぶことができます．

　特に，制御系解析ツールは技術者にとっては電卓のsin, cosと同じように単なる計算道具です．
難しい制御理論は後にして，とにかく使えるようにしておくと便利です．そういう意味で，だれでも
簡単に使える制御系解析ツールKMAPの普及活動に力をいれています．

ＫＭＡＰ(ケーマップ)は次のような機能を持っています．

＜新機能＞ＫＭＡＰゲイン最適化による多目的飛行制御設計(2)
　　設計目的①：アクチュエータを考慮
　　設計目的②：ゲイン余裕，位相余裕の要求値を満足して安定化
　　設計目的③：外乱応答のH∞ノルムを下げる(KMAP113～)

　飛行制御系の設計では，ゲイン余裕および位相余裕がスペックによって要求されています．このような
要求を満足する安定な制御系を得るために，H∞制御やLMIによる制御など数学的に複雑な方法が開発
されています．ところが，ここで紹介するＫＭＡＰゲイン最適化による方法を用いると，この種の多目的
設計問題を簡単に解くことができます．

　推力ベクタリングによるホバリング飛行の例題にて，下記資料でご紹介します．
ＫＭＡＰゲイン最適化による安定余裕要求を満足する多目的飛行制御設計

＜新機能＞ＫＭＡＰゲイン最適化による多目的飛行制御設計(1)
　　設計目的①：アクチュエータを考慮
　　設計目的②：制御系を安定化
　　設計目的③：外乱応答のH∞ノルムを下げる(KMAP111～)

　多目的飛行制御設計の方法としては， H∞制御，LMIによる制御，遺伝的アルゴリズム(GA)を用いた
最適化など各種方法が研究されていますが，いずれも数学的に難解であることから，一般のエンジニア
が簡単に利用するにはなかなか難しい方法と考えられます．

　このような多目的設計問題も，ここで紹介するＫＭＡＰゲイン最適化の方法を用いると簡単に
解くことができます．

　ＫＭＡＰゲイン最適化では，制御系を構成する際に“Z接続法”という方法を用います．これは
制御系の各要素の入出力にZ番号を与えて，それらを接続することでフィードバック制御系を構成
するもので，フィルタやフィードバックゲインを挿入した複雑な制御系を簡単な操作で構成する
ことができます．

　ＫＭＡＰゲイン最適化法とは，制御系内のフィルタやフィードバックゲインの組み合わせを設定して，
制御系における多目的の特性値を計算して最適解を求める方法です．ゲインの組み合わせ設定の方法と
しては，フィルタやゲインを適当に組み合わせて最適解を求めてもよいわけですが，これでは効率が悪
いので，本手法では乱数を用いてゲインの組み合わせを作り，繰り返し計算にて最適な解を求めるモン
テカルロ法といわれる方法です．繰り返し回数は100万回ですが，一般的なパソコンで数分程度が解が得
られます．

　推力ベクタリングによるホバリング飛行の例題にて，下記資料でご紹介します．
ＫＭＡＰゲイン最適化による多目的飛行制御設計

＜新機能＞要求値一覧表による飛行機の解析自動化 (KMAP106～)

　航空機関連を解析するためのＫＭＡＰの操作性を全面的に改良しました．これまで，解析内容
の全体がわかりにくい等のコメントもあり，解析項目の要求値等を一覧表として事前に設定する
方式にしました．
　実際の解析は，その一覧表のデータを選択して実行させるだけで，解析計算が自動的に行われ
ます．この方式の採用により，解析内容が明確となるとともに，計算実行も途中のキーイン操作
がないので簡単になりました.

＜新機能＞航空機の飛行制御系の解析が簡単にできるように
なりました(KMAP105～)

　これまで，飛行制御系を含んだ航空機の運動解析は，制御則といわれる舵面操舵ロジックを
インプットデータデータに組み込む必要がありました．例題のインプットデータをコピーして，
それをユーザーが修正して制御則を構築するやり方のみを採用していました．

　一方，飛行制御系の解析は，例えばダンパー機能やオートパイロットなどでは，ロジックは
基本的には同じような形式ですので，予め各種パターンの飛行制御則をそのまま利用した方が
効率がよく解析でき，ユーザーは簡単に解析作業に入ることができます．

　このような観点から，今回新バージョンKMAP105から，各種のパターンの制御則を選択できる
機能を追加しました．詳細は，【航空機の運動解析ＫＭＡＰの専用ホームページ】の使い方
および例題【４】＜飛行機の制御系解析＞の中に説明がありますのでご利用ください．

＜新機能＞航空機の翼理論, 2次元ポテンシャル流厳密解による解析
が可能になりました(KMAP104～)

　　図(a)　ジュコフスキー翼の流線 (迎角10°,ε=0.1, β=10°)

　　図(b) ジュコフスキー翼の翼上の流速 (迎角10°,ε=0.1, β=10°)

＜新機能＞航空機のスピン運動解析が可能になりました(KMAP101～)
「spin_motion.Y160806.wmv」をクリックすると，スピン運動が再生できます．

　このスピン運動解析は，通常の飛行機の運動解析とは空力係数の模擬方法が異なります．
スピン運動は，失速迎角を超えて非常に大きな迎角，および大きな横滑り角の運動となります．
従って，空力係数としてはその運動を模擬できるように入力する必要があります．

　具体的には，次の空力係数を用います．(下記番号を指定すると，空力係数のグラフがExcel
で表示することができます)
1 = ClDa, CmDf,　CnDa (α) (同じグラフ内)
2 = Clp,　Clr,　 CmDe　 (α) (同じグラフ内)
3 = Cnp,　CD0　　　　　 (α) (同じグラフ内)
4 = Cmq,　CmADOT　　 (α) (同じグラフ内)

18 = CD|De|(1/deg) (α)
19 = CD|Df|(1/deg) (α)
20 = CyDa　(1/deg) (α)
21 = Cyr　　(1/rad) (α)
22 = CLDe　(1/deg) (α)
23 = CLDf　(1/deg) (α)

24 = Cnr　 (1/rad) (α,De)
25 = CnDr　(1/deg) (α,De)
26 = ClDr　(1/deg) (α,De)
27 = CyDr　(1/deg) (α,De)

28 = Cl　　(1/deg) (α,β)
29 = Cm　　(-)　　　(α,β)
30 = Cn　　(1/deg) (α,β)
31 = Cy　　(1/deg) (α,β)
32 = CL　　(-)　　　(α,β)

　ここで，迎角α，横滑り角β，エレベータ舵角Deに関して次のようにデータを入力します．
　　　α＝-90°～90°を5°おきに 37点
　　　β＝ 0°,5°,10°,20°,30°の5点
　　　De＝押し舵最大，中立，引き舵最大の 3点
　下記に空力係数の例を示す．(迎角α＞0のスピン運動に対応)

　　　図(d)　スピン運動のタイムヒストリー例

　　図(e)　飛行機の運動変数の説明図

　KMAPでのスピン運動解析は，次の手順でおこないます．
　　①KMAPを立ち上げる
　　②「1 : 一般(下記以外) ⇒ 航空機の運動・制御系解析，スピン運動」を選択
　　③「3 : 例題ファイル(下記にリスト表示される)をコピー利用して新規作成」を選択
　　④「101 :(SPIN.航空機のスピン運動23.Y160805.DAT)」を選択
　　⑤「新しいファイル名を入力」
　この後は，画面の指示に従って操作してください．

＜新機能＞KMAP線図 (ブロック図の自動作画機能)が追加されました(KMAP92～)

　　　　　　　　図(a)　KMAP線図 (ブロック図の自動作画機能)

　このKMAP線図は，制御系のブロック図（下記の例参照）における信号の流れを，インプットデータとして
入力したものを順番に表示したもので，インプットデータにミスがないかを簡単にチェックできます．

　　　　　　　　図(b)　航空機のピッチ角制御系ブロック図の例
　　　　　　　　　　　　　（図(a)のKMAP線図に対応するもの)

＜基本的な機能＞

①飛行機の運動シミュレーション

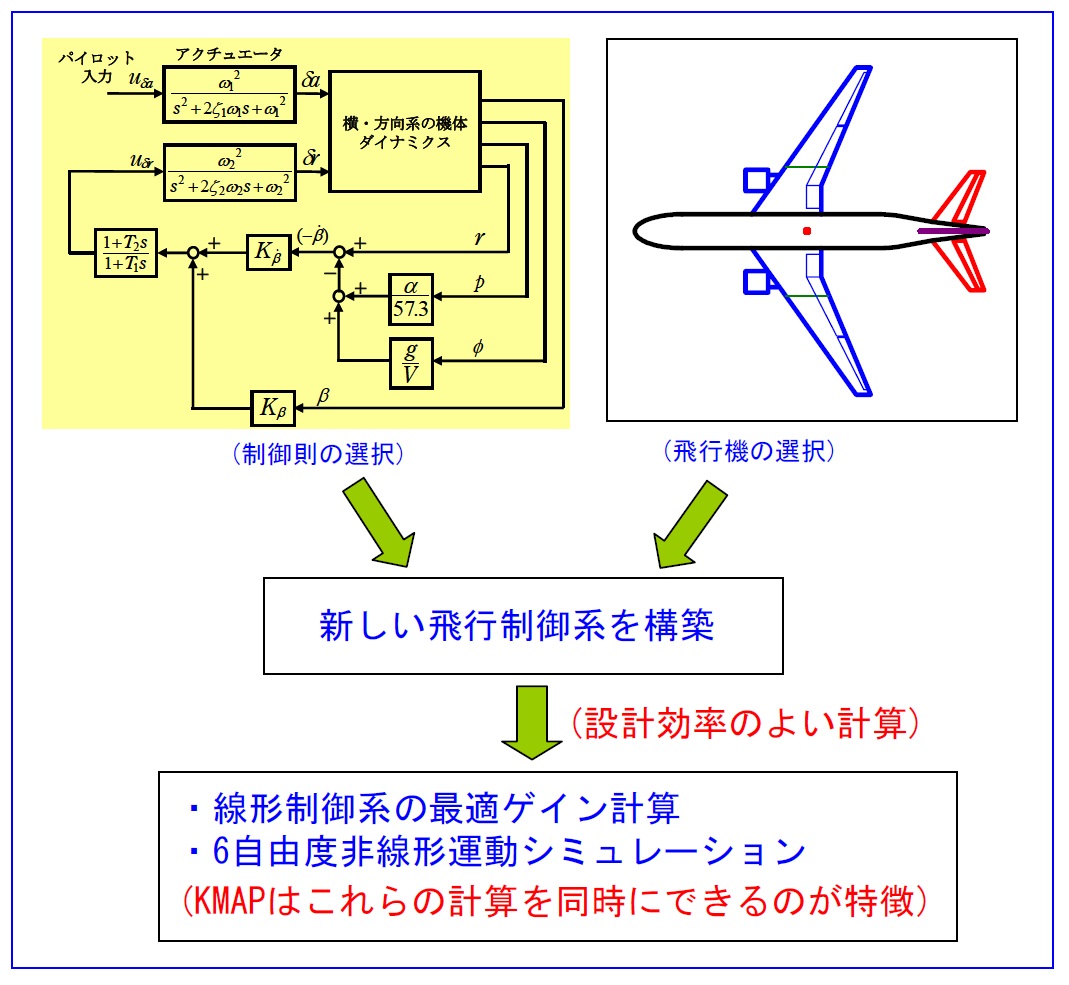
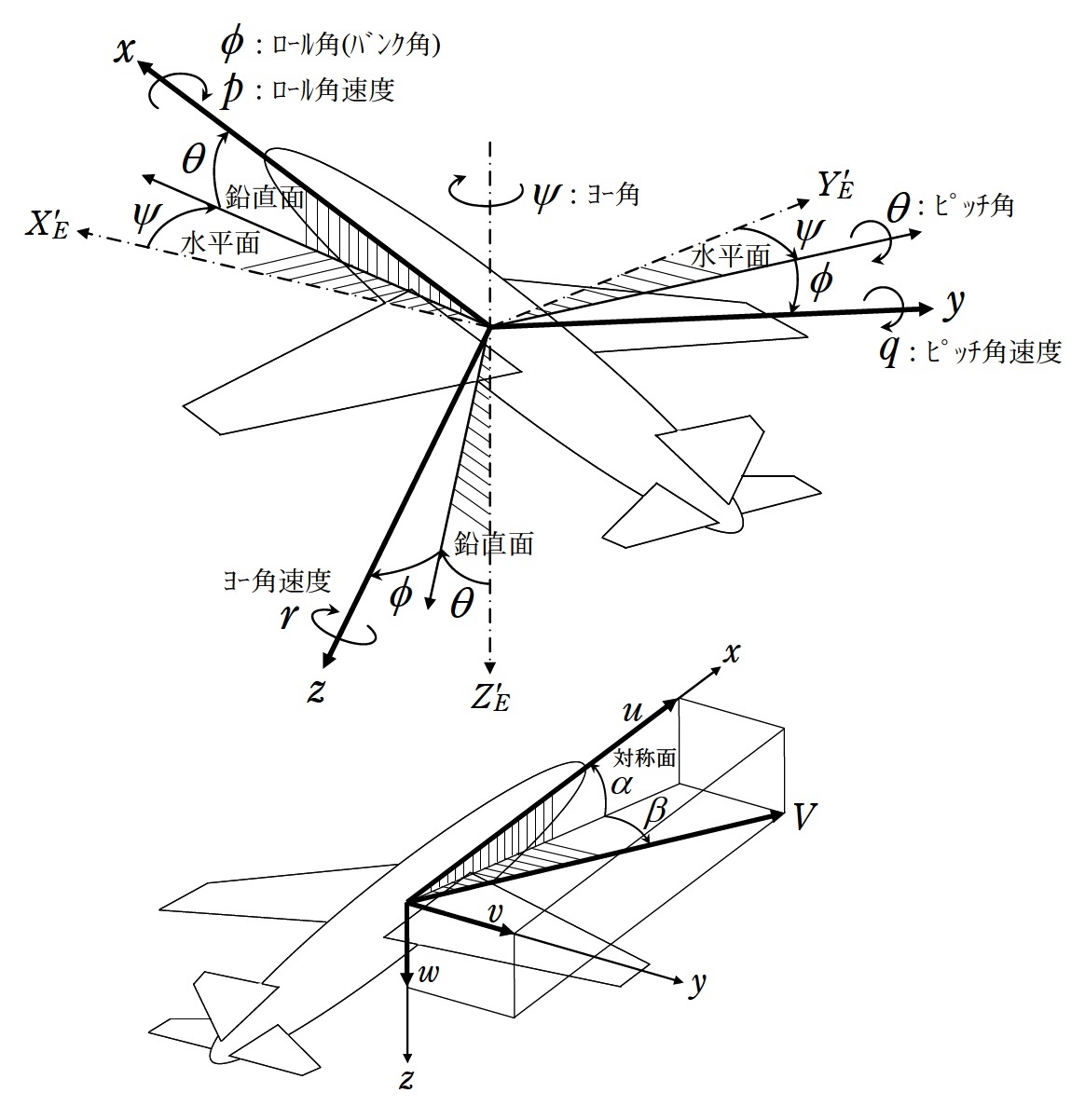
　機体諸元(重量，慣性モーメント等)，空力データ，制御則，パイロット操舵を入力することにより
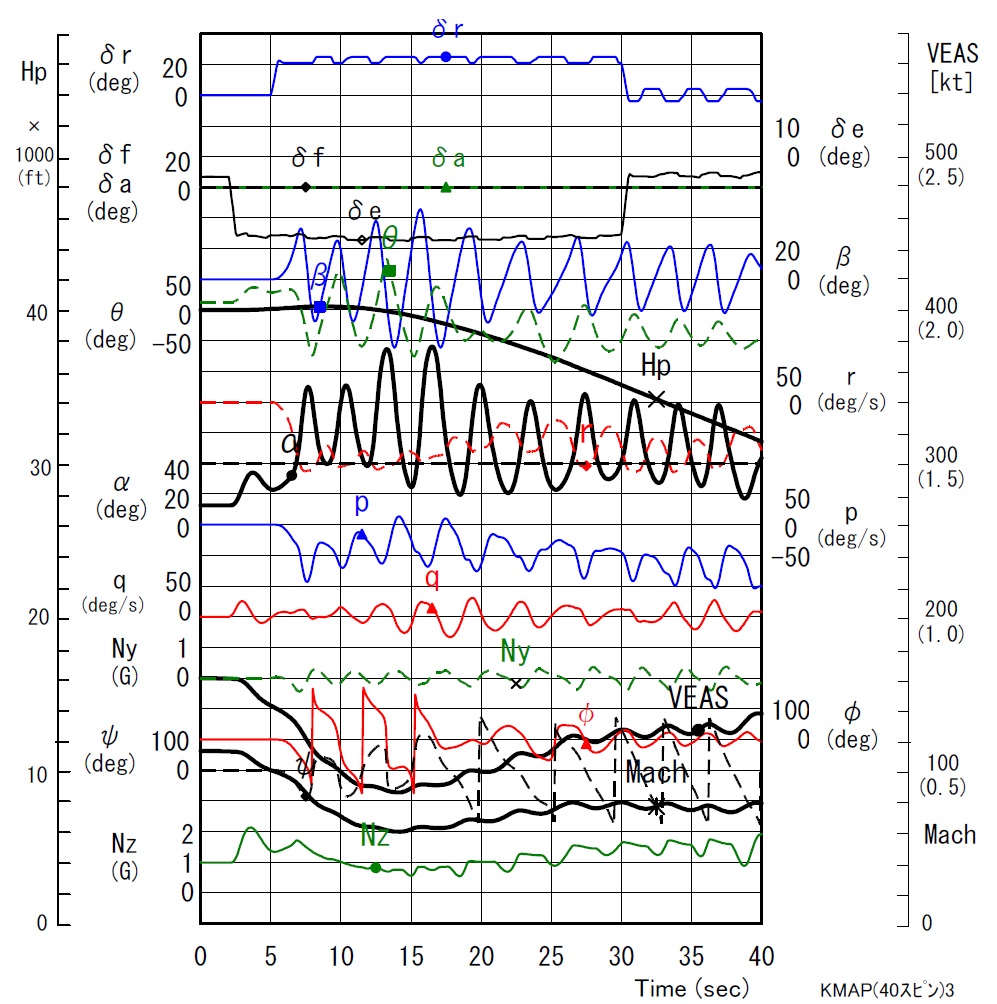
飛行機の運動がシミュレーションできます．ＫＭＡＰによる解析結果は，下記の図のようにExcel を
利用して表示することができます．Excel 図は各種メニューが用意されています．
(飛行機の三面図も簡単に描くことができます)

(下図のように飛行機の運動をアニメーションで確認できます)

「Duch_roll.wmv」をクリックすると，ダッチロール運動が再生できます．

「垂直離陸.wmv」をクリックすると，飛行機の垂直離陸の運動が再生できます．

「旅客機のホバリング.Y130609.wmv」をクリックすると，旅客機がホバリング後、
前進飛行から右旋回する運動が再生できます．

　運動解析プログラムＫＭＡＰは，飛行機の運動解析，制御系設計解析(古典制御から現代制御
まで)，飛行機の概念設計(含む空力微係数推算)などの各種解析が可能です．

　例えば，飛行機の運動方程式は知っていても自分でシミュレーションプログラムを作って解析
するのは簡単ではありません．たとえ計算できても正しい答えであるかの検証は難しい作業です．
ＫＭＡＰは飛行機の運動方程式は既にプログラム化されていますので，ユーザーは空力微係数，
機体諸元，アクチュエータ性能値などをインプットデータとして入力すれば直ちに運動シミュレ
ーションができます．

　また，飛行制御則もインプットデータにより定義することが可能です．ＫＭＡＰは入門者に
理論だけでなく，実際に計算を行うことで理解を深めて欲しいとの考えから開発したものです．
ユーザが簡単に使えるように適宜改善しています．

②飛行機の安定性･操縦性解析

　飛行機の飛行特性解析(安定性・操縦性の解析)についての詳細な検討結果が簡単に得られます．
安定性・操縦性の解析とは，飛行機の尾翼の設計に対応します．６自由度の運動方程式を解く
必要がありますので，これまでは時間のかかる作業でした．KMAPを用いると，性能要求を満足
する機体諸元(機体重量，主翼面積等)を求めた後，安定性・操縦性の解析を行い，設計基準を
満足するかどうかを表示します．

　具体的には，以下のような解析を行います．
　　【縦系の飛行特性解析】 (機体固有および制御系含み)
　　　①長周期モードの減衰比と振動数
　　　②速度安定の条件
　　　③飛行経路安定
　　　④短周期モードの減衰比と振動数
　　　⑤短周期モードのωsp･Tθ2
　　　⑥短周期モードの加速感度n/α
　　　⑦短周期モードのCAP (Control Anticipation Parameter)
　　　⑧縦静安定と重心後方限界
　　　⑨CAPによる重心後方限界
　　　⑩離陸引き起こしと重心前方限界
　　　⑪転覆角と重心後方限界
　　　⑫重心許容範囲と主脚位置

　　【横・方向系の飛行特性解析】 (機体固有および制御系含み)
　　　①ダッチロールモードの減衰比と振動数
　　　②ダッチロールの|φ/β|とζd･ωnd
　　　③ロールモードの時定数TR
　　　④スパイラルモードの振幅倍増時間T2
　　　⑤エルロン操舵時のロール角速度振動
　　　⑥ロール性能
　　　⑦定常横滑り能力

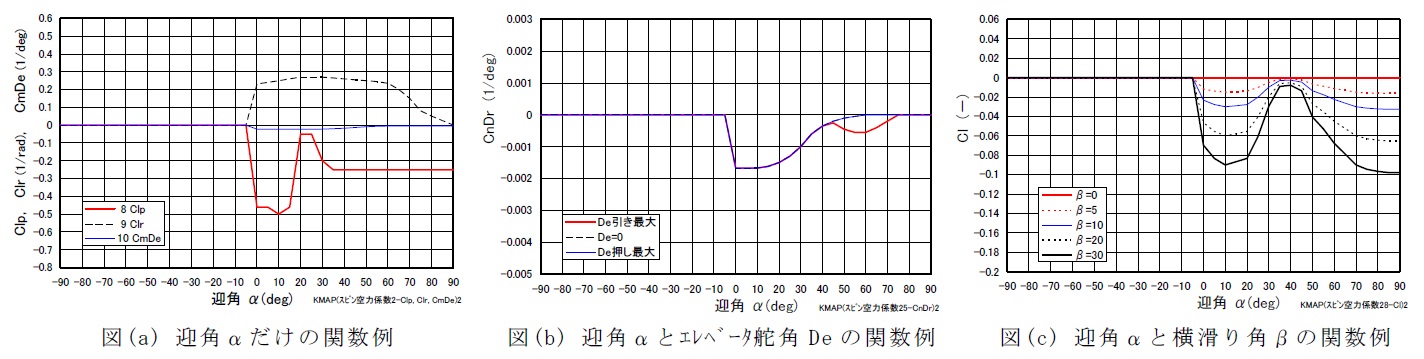
　　　　　　　　定常横滑り能力の例 (横滑り角β=10°)

　これらの飛行特性解析は，機体固有と制御系含みの２つの場合について，解析結果を表示し
ます．特に，制御系を含んだ場合の飛行特性解析はこれまで難しい領域でしたが，KMAPでは
自動的にシミュレーション計算等を行って解析を可能にしました．飛行機設計の時間が大幅
に短縮できます．

③飛行機の空力データの推算

　与えられた機体形状に対して空力データを推算して出力します．

④飛行機の概念設計と３面図作成

　与えられた機体形状に対して空力データを推算し，性能要求値を満足する機体諸元
(重量，翼面積等)を出力し，設計結果を３面図として表示します．模型飛行機から旅客機
まで各種飛行機を設計できます．

(下記の機体３面図は，KMAPの解析結果で描いたものです．)

　例として，800人乗りの超大型旅客機を試設計してみましょう．航続距離15,000km，離陸
滑走路長3,000m以下，着陸滑走路長2,000m以下としてＫＭＡＰで設計した結果は次のように
なりました．

　　　航続距離 R =15,000km
　　　離陸滑走路長 sTO= 3,000m
　　　着陸滑走路長 Ld= 1,620m
　　　接地速度 VTD= 120kt

　　　離陸重量 WTO = 543tf
　　　着陸重量 WLD = 319tf
　　　自重 Wempty= 225tf
　　　燃料重量 Wfuel = 238tf
　　　ﾍﾟｲﾛｰﾄﾞ Wfixed= 80tf
　　　離陸推力 (T)to= 118tf

　　　主翼面積 S = 824 m2
　　　スパン b = 78.6m
　　　アスペクト比 A = 7.5
　　　平均翼弦 CBAR= 11.4m
　　　前縁後退角 ΛLE= 41deg
　　　翼面荷重 WTO/S= 659kgf/m2
　　　推力重量比(T/W)to= 0.218

　このように，離陸重量543ﾄﾝ，スパン(翼幅)78.6mの機体が得られました．ＫＭＡＰでは
３面図も上記のように簡単に描くことができます．

　また，ＫＭＡＰでは設計と同時に空力微係数が推算されます．

　　　＜空力微係数推算結果（着陸形態）＞
　　　 CLα=0.1012(1/deg).........................Cyβ=-0.01584(1/deg)
　　　 CLδe=0.00540(1/deg)....................Cyδr=0.00304(1/deg)
　　　 CLδf=0.0237(1/deg).......................Clβ=-0.00463(1/deg)
　　　 Cmα=-0.0272(1/deg).....................Clδa=-0.001138(1/deg)
　　　 Cmδe=-0.0203(1/deg)...................Clδr=0.0001355(1/deg)
　　　 Cmδf=-0.00743(1/deg).................Clp=-0.419(1/rad)
　　　 Cmq=-27.0(1/rad)..............................Clr=0.321(1/rad)
　　　 Cmαdot=-8.57(1/rad).....................Cnβ=0.00300(1/deg)
　　　 k=0.0518(－).........................................Cnδa=-0.0000208(1/deg)
　　　 CD0(F/UP,G/UP)=0.01667(－).....Cnδr=-0.001613(1/deg)
　　　 CD0(F/DN,G/DN)=0.0507(－).......Cnp=-0.00438(1/rad)
　　　 CD|δf|=0.001202(1/deg)................Cnr=-0.293(1/rad)

. この空力微係数を用いて，ＫＭＡＰ内では飛行特性解析，制御則設計，シミュレーションなど
各種の解析が簡単に行えます．

⑤一般制御系の設計解析

　飛行機以外の一般の制御系の設計解析も可能です．
　　極・零点配置
　　根軌跡
　　ボード線図
　　ベクトル軌跡
　　各種フィルタ演算
　　固有値計算
　　リカッチ方程式計算
　　最適制御
　　H∞制御
など，古典制御から現代制御までの種々の設計法が準備されています．

　下記に航空機のピッチ角制御におけるＬＱＩ（サーボ系）の例を示します．縦系のピッチ
角コマンドθm に対して機体のピッチ角θ を追従させる積分型最適制御系です．

　　　　　　　　　飛行機のピッチ角ＬＱＩ最適制御ブロック図
　　　　　（このブロック図をクリックすると大きく見ることができます）

　このときのシミュレーション結果を次に示します．ピッチ角θが目標値に良好に追従して
いる様子がわかります．
　(詳細は，本の紹介(3)をご覧ください)

⑥Z接続法による制御系設計ツールについて

　Z接続法とは，制御系の情報をZ変数でつなぐことで制御系を構成していく方法です．
これによって構成された制御系は，ＫＭＡＰツールを用いてシステムの極・零点配置や周波
数特性などを良好な特性にすることができます．

　一般的に，システムの特性を表す伝達関数(入力に対する出力の特性をラプラス変換した
もの)は上記のように，積分，１次遅れ，ハイパス，リードラグ，2次遅れ，2次遅れの微分，
ノッチフィルタの要素の組み合わせで表すことができます．Z接続法では，この原理により，
これらの各要素の入出力にZ番号を付与して，システム要素間の情報の流れを加減算すること
によって制御系を作り上げるものです．例題をいくつかご紹介します．

【例題１】航空機のラダー系の安定化制御

　　　　　　　　　図1　航空機のラダー制御系ブロック図

　図1に示すラダー制御系について，ゲインＫとリードラグ時定数Ｔ1およびＴ2を，Z接続法
ゲイン最適化によりシステムを安定化するように決定してみましょう．ＫＭＡＰのインプッ
トデータは次のように簡単です．図1のブロック図を順番にZ番号で接続していくだけです．
このデータの後に，求めるゲインが記述してある行数を定義しておきます．このケースでは，
92,93,94行目です．

　ゲイン探索の範囲を指定して解析を実行すると，100万回のゲインの組み合わせの中から
最適解を表示します．図2は安定解の存在範囲で，図の中の黒い点が極の位置を示しています．

　　　　　　　　　　　　図2　安定な極の存在範囲

　得られたゲインを用いて，図1のRGAINを変動させて描いた根軌跡が図3です．左半面45°の
非常に安定した位置に極が移動していることがわかります．

　　　　　　　図3　Z接続法ゲイン最適化により得られた根軌跡



　このように，ＫＭＡＰを用いたZ接続法ゲイン最適化手法により，安定な制御系が簡単に
設計できますので，ぜひ使ってみてください．

⑦船の運動解析

　下記の船の運動（付加質量，付加慣性モーメントを考慮）解析も可能です．

⑧自動車の運動解析

　下記は自動車の外乱運動特性の例です．

⑨ロボットの制御

　下記の２リンクマニピュレータ制御系解析も可能です．

⑩工作機械の制御

　下記の工作機械の位置決め制御系解析も可能です．

⑪振動工学の解析
　下記の自動車の上下回転運動などが簡単に解析できます．

⑫構造物の弾性解析

　下記は有限要素法による片持ちはりの曲げ解析の例です．

⑬流体力学の解析

　下記は差分法による円柱まわりの流れの解析例です．

⑭最適化の解析法

　下記は準ニュートン法を用いた最適制御の解析例です．

　ＫＭＡＰの専用ホームページに戻る　

片柳亮二博士のホームページへ

(片柳亮二)